Universität Hamburg - der Forschung, der Lehre, der Bildung, zur Homepage
Integrated Climate Data Center
CENIntegrated Climate Data Center ICDC

Foto: getty images/L. Calvetti

Ozeangezeiten aus dem Datenassimilationsmodell HAMTIDE

Hamtide Amplitude m2
HAMTIDE global Phase of m2 constituent.
HAMTIDE globale Amplitude und Phase des m2-Bestandteils . Copyright: UHH/CEN/AJB

Übersicht

Zugang

UNEINGESCHRÄNKT:

EINGESCHRÄNKT: Dieser Link auf den Datensatz ist nur für eine eingeschränkte Nutzergruppe verfügbar.  Der Datensatz ist nur im CEN/MPI Netzwerk bzw. von außen mit Kundenkonto  zugreifbar.  Bitte wenden Sie sich an ICDC, wenn Sie von außerhalb des Netzwerks auf diese Daten zugreifen möchten.

  • Datenzugriff über Filesystem: /data/icdc/ocean/hamtide

nach oben

Beschreibung

Alle numerischen Modelle sind fehlerbehaftet und deren Resultate deshalb unvollständig. Speziell bei Gezeitenmodellen können viele Probleme auftreten, was unbekannte Dissipationsparameter [Taguchi et al., 2010], eine ungenaue Bathymetrie, Unsicherheiten in Anfangs- und Randbedingungen und eine fehlende Physik betrifft - insbesondere in Flachgewässern [Taguchi, 2004; Setiawan, 2007, siehe Referenzen]. Die Begrenzung der Gezeitenmodelle durch geophysikalische Daten reduziert dieses Defizit und kann dabei helfen, die fehlende Physik oder unsichere Parameter zu bestimmen. Jedoch weisen konventionelle Datenassimilationsmethoden Schwierigkeiten mit der schnell wachsende Anzahl von Altimeterdaten und vor allem mit der Reproduktion der nicht-linearen Gezeiten in Flachwasserregionen auf. Das Gezeitenmodell HAMTIDE (Hamburg direct data Assimilation Methods for TIDEs) des Instituts für Meereskunde der Universität Hamburg wurde entwickelt, um diese Probleme zu bewältigen, spart Ressourcen und liefert präzise Ergebnisse.

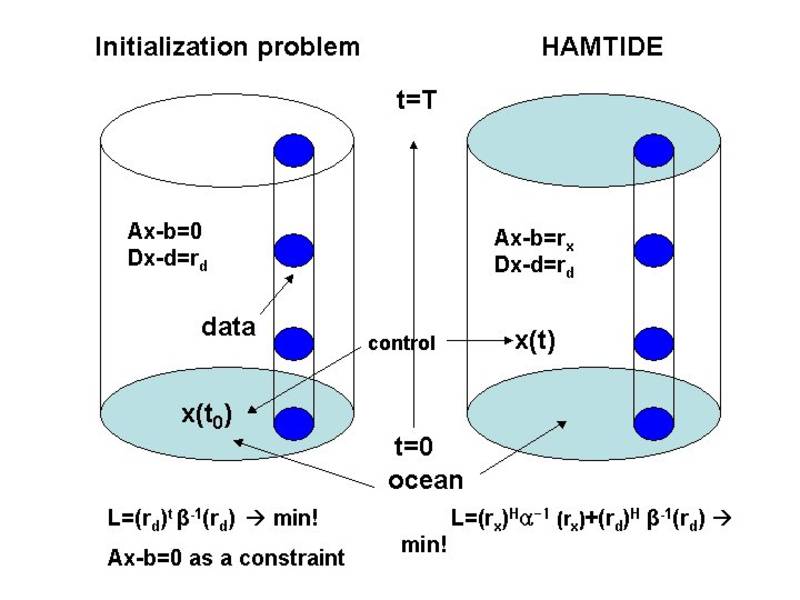
Schematic variational techniques with strong (left) and weak (right) formulation.
Abb. 1: Schema des Variationsverfahren mit starker (links) und schwacher (rechts) Zwangsbedingungen. Effektive Gewichtsmatrizen α und β müssen definiert werden.

Seit den frühen 90ern wurden generalisierte inverse Methoden für Tiden an der Universität Hamburg entwickelt [Zahel, 1995]. Das Prinzip von HAMTIDE ist die direkte Minimierung des Modellfehlers und der Ungenauigkeit der Messungen nach der Methode der kleinsten Quadrate, was in der Lösung der überbestimmten algebraischen Gleichungen und der so genannten Normalengleichung resultiert. Die Gleichungen werden dann durch eine arbeitsspeichersparende, iterative Methode für die gegebene dünnbesetzte Matrix gelöst. Gleichzeitig wird das Modell durch Ableiten der Physik aus den Daten korrigiert. Die dynamischen Residuen werden dann zur Detektion möglicher Modellfehler wie Parametrisierung der Dissipation, AuflastundSelbstanziehung (loading and self-attraction - LSA) und Ungenauigkeiten in der Bathymetrie genutzt [Taguchi et al., 2010, siehe Referenzen]

Die direkte Methode unterscheidet sich von gewöhnlichen Anfangswertproblemen wie das quasi-geostrophische Ozeanmodell, dessen Anfangsbedingungen als freie Parameter (Controls) variiert werden, während das Modell als starke Zwangsbedingung genutzt wird und das Variationsverfahren normalerweise als Lösungsansatz dient(Abb. I). Auf der anderen Seite stellt die direkte Methode die Korrektheit der Dynamik (schwache Zwangsbedingung) und der Daten in Frage (Abb. I). Deshalb werden alle Variablen x (für die gesamte Tidenperiode) des Modells in Betracht gezogen und angepasst, bis der Abstand der Messungen zu den Modellentsprechungen ein Minimum erreicht und das Extremum der gewichteten Summe der Dynamik- und Datenresiduen erreicht wird.

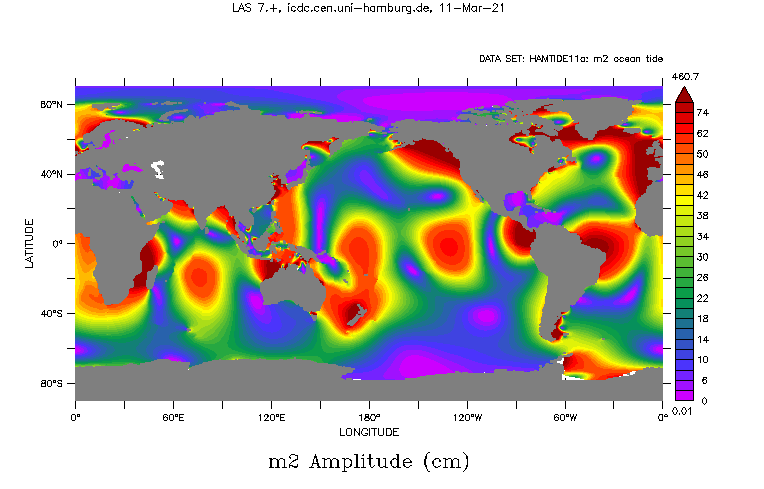
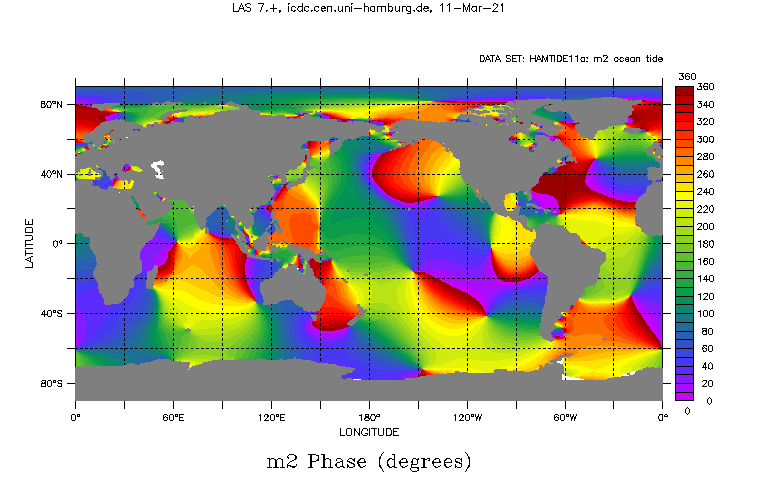
HAMTIDE wird in einer räumlichen Auflösung von 7,5 Grad betrieben. Dessen Lösungen werden durch Daten von Satellitenaltimetermissionen aus der DGFI Altimeterdatenbank eingeschränkt, die aus der 15-jährigen Zeitreihe von TOPEX and Jason-1 gespeist wird [Bosch et al., 2009]. Die Altimeterdaten wurden in Form einer empirischen Analyse von cross-kalibrierten Satelliten-Altimeterdaten mehrerer Missionen in Form von M2, S2, N2, K2, K1, O1, Q1, P1 und 2N2 Komponenten zur Verfügung gestellt.

Amplitude (AMPL) und Phase (PHAS) des Wasserstandes ζ(x,y) werden in einer komplexen Zahlen angegeben:

ζ(x,y) = RE + i * IM,

wobei  RE = AMPL * cos(PHAS) und IM = AMPL * sin(PHAS) und sie sind wie im folgenden Beispiel in der ASCII-Datei angeordnet:

Reihenfolge der Zahlen
LONLATREIMAMPLPHAS
324.000 83.625 0.4718 3.1347 3.17 81.44

Verfügbare Tiden

Astronomische semidiurnal Tiden:

  • M2: Principal lunar,
  • S2: Principal solar,
  • N2: Larger elliptical lunar,
  • K2: Declinational solar/lunar,
  • 2N2: Second-order elliptical lunar

Astronomical diurnal tides:

  • K1: Principal solar/lunar,
  • O1: Principal lunar,
  • P1: Principal solar,
  • Q1: Larger elliptical lunar

Dieser Datensatz ist ein ICDC-Produkt. Danksagungen: Dieses Projekt wurde von der Deutschen Forschungsgemeinschaft (SPP1257) finanziert.

Letzte Aktualisierung des Datensatzes am ICDC:

nach oben

Parameter

Parameter des HAMTIDE Datensatz
NameEinheit
Amplitude cm
Phase (Greenwich) Grad (º)

nach oben

Abdeckung, räumliche und zeitliche Auflösung

Zeitraum und zeitliche Auflösung:

  • Kein Zeitraum; Modell / Assimilationsresultat, in das 15 Jahre Daten eingeflossen sind
  • Keine zeitliche Auflösung

Räumliche Abdeckung und Auflösung:

  • Global
  • Räumliche Auflösung: 7,5' x 7.5', kartesisches Gitter
  • Geographische Länge: 0.0°E bis 360°E
  • Geographische Breite: -90.0°N bis 90.0°N
  • Dimension: 1441 Zeilen x 2881 Spalten
  • Höhe: 0.0 m

Format:

  • NetCDF

nach oben

Datenqualität

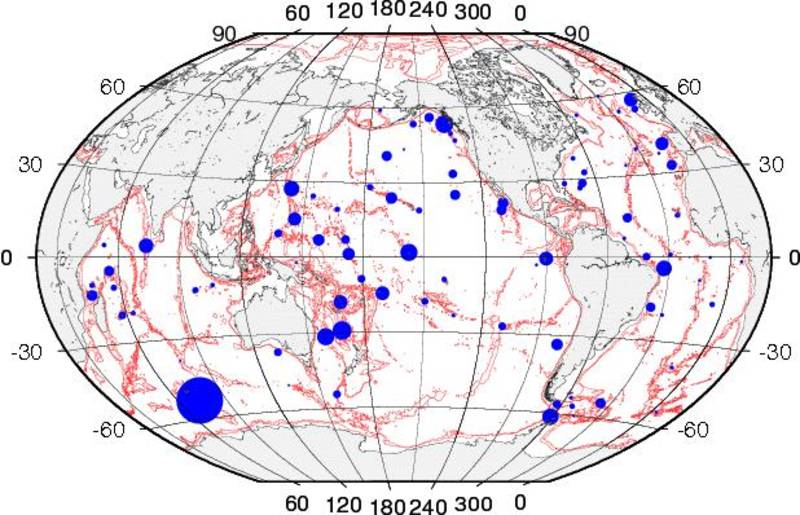
HAMTIDE RMS differences of M2
Abb. 2: RMS-Differenzen der M<sub>2</sub>-Tidenkonstanten zwischen dem ST102p Datensatz und HAMTIDE mit einer Gitterauflösung von 7.5'. Der Durchmesser der blauen Kreise ist proprtional zur RMS-Differenz. Die dünnen roten Linien stellen die Konturlinien in 2000 und 4000 Meter Ozeantiefe dar [Taguchi et al., 2010].

Vergleiche zwischen HAMTIDE und pelagischen Referenzdaten (Abb. 2), Vergleiche zu ST102p von R. Ray [2007], und auch dem FES Gezeitenmodell [Lyard et al., 2006] wurden vorgenommen, in dem beispielhaft die M2, S2, N2, K2, K1, O1, Q1, P1 und 2N2 Hauptkomponenten betrachtet wurden.

Hinweis: das FES Modell assimiliert den ST102p Datensatz, wobei das HAMTIDE Modell lediglich Altimeterdaten assimiliert. Die RMS-Differenzen zwischen HAMTIDE und FES2004 für 9 Komponenten unterscheiden sich jedoch innerhalb von 1mm an den ST102p Pegelstationen.

.

RMS-Differenzen (in cm) zwischen ST102p Datensatz und HAMTIDE/FES2004 Modellergebnissen.
ModelAuflösungM2S2N2K2K1O1P1Q12N2
HAMTIDE 7.5’ 1.5 1.0 0.7 0.4 1.1 0.8 0.4 0.3 0.3
FES2004 - 1.4 0.9 0.7 0.5 1.0 0.7 0.4 0.3 0.3

nach oben

Kontaktperson

Remon Sadikni
ICDC / CEN / University of Hamburg
E-Mail: remon.sadikni"AT"uni-hamburg.de

nach oben

Referenzen

Literatur:

  • Bosch B., R. Savcenko, F. Flechtner, C. Dahle, T. Mayer-Gürr, D. Stammer, E. Taguchi, and K-H. Ilk (2009), Residual ocean tide signals from satellite altimetry, GRACE gravity fields, and hydrodynamic modeling, GJI, 178(3), 1185-1192. doi :10.1111/j.1365-246X.2009.04281.x. https://doi.org/10.1111/j.1365-246X.2009.04281.x
  • Lyard, F., F. Lefevre, T. Letellier, and O. Francis (2006), Modelling the global ocean tides: a modern insight from FES2004, Ocean Dynamics, 56(5-6), 394-415, doi:10.1007/s10236-006-0086-x. https://doi.org/10.1007/s10236-006-0086-x
  • Ray R. G. (2007), ST102p data set, personnel communication
  • Setiawan, A. (2007), Modelling Over- and Compound Tides of the Irish and Celtic Seas using Variational Data Assimilation Methods, Thesis, University of Hamburg, Hamburg, Germany, https://ediss.sub.uni-hamburg.de/handle/ediss/1837
  • Taguchi, E. (2004), Inverse Modellierung nichtlinearer Flachwassergezeiten und ihre Anwendung auf ein Randmeer, Berichte aus dem Zentrum fuer Meeres- und Klimaforschung,47. https://ediss.sub.uni-hamburg.de/handle/ediss/419
  • Taguchi, E., Stammer, D., and Zahel, W. (2014), Inferring deep ocean tidal energy dissipation from the global high-resolution data-assimilative HAMTIDE model, J. Geophys. Res. Oceans, 119, 4573– 4592, https://doi.org/10.1002/2013JC009766
  • Zahel, W. (1995), Assimilating ocean tide determined data into global tidal models. J. Mar. Syst. 6, 3-13, doi:10.1016/0924-7963(94)00014-3. https://doi.org/10.1016/0924-7963(94)00014-3

nach oben

Datenzitat

Bei Verwendung der Daten diese bitte wie folgt zitieren:

Taguchi, E., Stammer, D., and Zahel, W. (2014), Inferring deep ocean tidal energy dissipation from the global high-resolution data-assimilative HAMTIDE model, J. Geophys. Res. Oceans, 119, 4573– 4592, https://doi.org/10.1002/2013JC009766

Distributed in netCDF format by the Integrated Climate Data Center (ICDC), CEN, University of Hamburg, Hamburg, Germany.

nach oben